This is always true with real numbers, but not always for imaginary numbers We have ( x y) 2 = ( x y) ( x y) = x y x y = x x y y = x 2 × y 2 (xy)^2= (xy) (xy)=x {\color {#D61F06} {yx}} y=x {\color {#D61F06} {xy}}y=x^2 \times y^2\ _\square (xy)2 = (xy)(xy) = xyxy = xxyy = x2 ×y2 For noncommutative operators under some algebraicZiddhu ziddhu 2612 Math Secondary School Find the extreme value of the function f(x,y) = xy x^2 y^2 2x 2y 4 1 See answer ziddhu is waiting for your help Add your answer and earn pointsFree PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystep

Systems Engineering And Analysis Ppt Download
F(x y)=xy-x^2-y^2-2x-2y 4
F(x y)=xy-x^2-y^2-2x-2y 4-Find the extreme value of the function f(x,y) = xy x^2 y^2 2x 2y 4 Get the answers you need, now!X2 − 2xy y2 − 4 x 2 2 x y y 2 4 Factor using the perfect square rule Tap for more steps Check the middle term by multiplying 2 a b 2 a b and compare this result with the middle term in the original expression 2 a b = 2 ⋅ x ⋅ ( − y) 2 a b = 2 ⋅ x ⋅ ( y) Simplify 2 a b = − 2 x y 2 a b = 2 x y



The Factors Of X 2 4y 2 4y 4x Y 2x 8 Are A X 2y 4 X 2y 2 B X Y 2 X 4y 4 C Youtube
Answer to The critical points for f(x, y) = xy x^2 y^2 2x 2y 4 are A, (1, 1) min, (2, 1) max B, (2, 2) min C, (2, 2 Skip Navigation Chegg homeAnswer to Given the function f(x,y)=4xy^2x^2y^2xy^3 (a) Find and classify all the critical points (b) Find the absolute maximum and minimumOf course, (b) is the complete factorization, (a) is not Comparing the results in (a) and (b), we can get x 4 x 2 y 2 y 4 = (x 2 xy y 2)(x 2 –xy y 2)
This is the graph of y = f(x) First I want to label the coordinates of some points on the graph Since, for each point on the graph, the x and y coordinates are related by y = f(x), I can put the coordinates of these points in a list x y = f(x)4 1 1 1 2 0 311) is a critical point The second derivative test f xx = 2;f yy = 2;f xy = 0 shows this a local minimum withFree equations calculator solve linear, quadratic, polynomial, radical, exponential and logarithmic equations with all the steps Type in any equation to get the solution, steps and graph
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyFind the extreme values of f(x,y)=x 22y2 on the disk x2y ≤1 •Solution Compare the values of f at the critical points with values at the points on the boundary Since f x =2x and f y =4y, the only critical point is (0,0) We compare the value of f at that point with the extreme values on the boundary from Example 2 •f(0,0)=0 •f(±1,0)=1Jun 17, 18 · Please see the explanation below The function is f(x,y)=x^2xyy^23x3y4 The partial derivatives are (delf)/(delx)=2xy3 (delf)/(dely)=2yx3 Let (delf)/(delx)=0 and (delf)/(dely)=0 Then, {(2xy3=0),(2yx3=0)} =>, {(x=3),(y=3)} (del^2f)/(delx^2)=2 (del^2f)/(dely^2)=2 (del^2f)/(delxdely)=1 (del^2f)/(delydelx)=1 The Hessian matrix is Hf(x,y)=(((del^2f)/(delx^2),(del^2f)/(delxdely)),((del^2f)/(delydelx),(del^2f)/(dely^2))) The determinant is D(x,y)=det(H(x,y))=(2,1),(1,2) =4



Implicit Differentiation Advanced Example Video Khan Academy



Answered Linear Equations 26 Chapter 1 Problems Bartleby
Add '2y' to each side of the equation x 2y 2y = 0 2y Combine like terms 2y 2y = 0 x 0 = 0 2y x = 0 2y Remove the zero x = 2y Simplifying x = 2y Subproblem 2 Set the factor '(2x 1y)' equal to zero and attempt to solve Simplifying 2x 1y = 0 Solving 2x 1y = 0 Move all terms containing x to the left, all other terms toF (xy)f (x) = f (y) 2xy If we divide both sides by y, and take the limit of both sides, as y approaches 0, we get f' (x)= 2x (limit as y→0) f (y)/y Since f (0) is 0 from the initial conditions (put x=y=0 in the original expression), we have a 0/0Subject to the constraint 2x2 (y 1)2 18 Solution We check for the critical points in the interior f x = 2x;f y = 2(y1) =)(0;



Pde Tutorial Sheet



Show That F X Y X 2ye X 2 Y 2 Has Maximum Values At 1 1 2 And Minimum Values At Show Also That F Has Infinitely Many Other Critical Points And D 0 At
X2y=1;2xy=4 Simple and best practice solution for x2y=1;2xy=4 Check how easy it is, to solve this system of equations and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework(b) x 6 – y 6 = (x 3) 2 – (y 3) 2 = (x 3 y 3)(x 3 – y 3), by (1) = (x y)(x 2 – xy y 2)(x y)(x 2 xy y 2), by (2) and (3) Which of the above factorization is correct?Multiply \frac {y^ {2}2xyx^ {2}} {x^ {2}y^ {2}} times \frac {2x} {xy} by multiplying numerator times numerator and denominator times denominator Cancel out x in both numerator and denominator Factor the expressions that are not already factored Cancel out xy in both numerator and denominator



The Factors Of X 2 4y 2 4y 4x Y 2x 8 Are A X 2y 4 X 2y 2 B X Y 2 X 4y 4 C Youtube



Discuss The Maxima And Minima Of The Function U X 3y 2 1 X Y Answer Mathematics 1 Question Answer Collection
Sep 10, 17 · 1/f df/dx = dy/dx ln2, df/dx = f ln 2 dy/dx= 2ŷ ln 2 dy/dx Put all to gether derivative is ln2 2^x ln 2 2^y dy/dx =ln2 2^x dy/dx dy/dx ( 12^y ln 2)=0 Since bracket can not be 0, dy/dx=0 Show more iceman Lv 7Feb 17, 17 · Explanation The theory to identify the extrema of z = f (x,y) is Solve simultaneously the critical equations ∂f ∂x = ∂f ∂y = 0 (ie zx = zy = 0) Evaluate f xx,f yy and f xy( = f yx) at each of these critical points Hence evaluate Δ = f xxf yy − f 2 xy at each of these points Determine the nature of the extrema;Problem 12 Easy Difficulty If $ f(x, y) = \sqrt{4 x^2 4y^2} $, find $ f_x(1, 0) $ and $ f_y(1, 0) $ and interpret these numbers as slopes Illustrate with either handdrawn sketches or



Limits And Continuity Pdf Free Download



Solve The Following Systems Of Equations X Y 2 And 2x 2y 4 Brainly In
How to solve Find all local extreme values for A) f(x, y) = xy x^2 y^2 2x 2y 4 B) g(x, y) = 3y^2 2y^3 3x^2 6xy By signing up,We know that $(x2y)(x2y)=4$ and that $(x2y)(x2y)=x^24y^2$ Thus, Quantity A MUST be equal to $4$, which is less than Quantity B The correct answer is B, Quantity B is greater What Did We Learn Coincidental mathematical relationshipsClearly 6= 0 It follows that x= 3 and y= 4 Using the constraint, x 2 y = 25 9 2 16 = 25 25 2 = 25 2 = 1 = 1 The points of interest are (x;y) = (3;4) Therefore, the maximum and mimimum values are f(3;4) = 50 and f( 3;
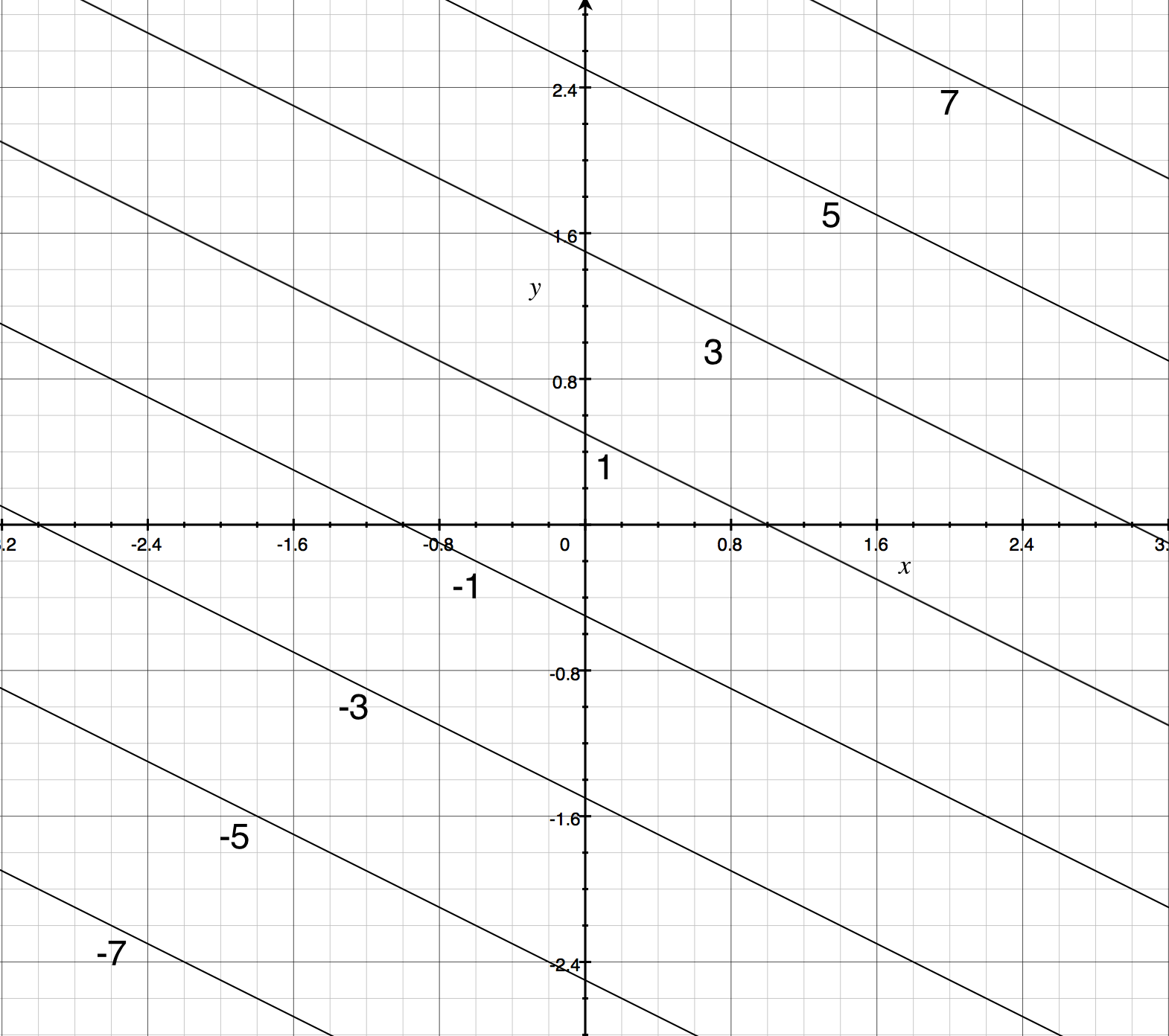


Contour Maps Article Khan Academy



The Factors Of X 3 X 2y X Y 2 Y 3 Are A X Y X 2 X Y Y 2 B X Y X 2 X Y Y 2 C Youtube
Learn to factorise an expression of the form x^4 x^2y^2 y^4 This is solved by adding and subtracting x^2y^2 to the given expression and reducing it to tF(x,y)=xy over the region D = {(x,y) x2 y2 8} As before, we will find the critical points of f over DThen,we'llrestrictf to the boundary of D and find all extreme values It is in this second step that we will use Lagrange multipliers The region D is a circle of radius 2 p 2 • fx(x,y)=y • fy(x,y)=xIf f(x;y) can be made arbitrarily close to L by taking (x;y) su ciently close to (a;b) Note Recall that lim x !a f(x) exists if and only if lim x a f(x) = lim f(x) We can only approach x = a from two directions However, for functions of two variables, there are in nitely many



Ex 3 2 4 Which Of The Pairs Of Linear Equations Are Ex 3 2



Answered 14 F X Y Z X Y 4z X Y Bartleby
Dec 09, 11 · (a) Find y' by implicit differentiation (b) Solve the equation explicitly for y and differentiate to get y' in terms of x (c) Check that your solutions to part (a) and (b) are consistent by substituting the expression for y into your solution for part (a)Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor1st x2y=0 2nd y=2x3Rewrite 2nd as follows 3rd 2xy=3 Multiply 1st by 2 to get 4th 2x4y=0 Subtract 4th from 3rd to get 5th 3y=3 y=1 Substitute this value into 1st to solve for x x2(1)=0 x=2 Solution (2,1) Cheers, Stan H



Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange



Solve For Lines Of Equation X Y 5 0 And 2x 2y 10 0 Youtube
X2 y2 = 1 xy Use Equation 2 to substitute into the equation for y '' , getting , and the second derivative as a function of x and y is Click HERE to return to the list of problems SOLUTION 14 Begin with x2/3 y2/3 = 8 Differentiate both sides of the equation, getting D (JNTU BTech M2 Maths and Bsc Maths Chapter Partial Differentiation Topic Maximum and MinimumExamine the function f(x ,y)=x^4y^42x ^24xy2y^2 for extI should solve the following system $$\begin{cases} x^4x^2y^2y^4=21 \\ x^2xyy^2=3 \end{cases}$$ by reducing the system to a system of second degree What can I



Engineering Mathematics Notes



Homework 5 1
Jul 17, 17 · x = y If y is a root, then (x y) is a factor Since it is the only one, then the quadratic is a perfect square (as indicated by the 0 under the square root) x^2 2xy y^2 = (x y)(x y) = (x y)^2"y is a root" simply means that the only way we can get the thing to add up to zero, is to make x = y for example, if x = 3 and y = 3On f(x 2 y 2) = f(x) 2 f(y) 2 Consider an integervalued function f(k) such that f(1) is positive and We can show that the only such function is the identity function f(k) = k To prove this, first note that setting m = 1 and n = 0 in equation (1) and rearranging terms gives the conditionSea F(x) = 4x 3 y g (x) =x_x2 Halla F(2) luisjoseolivas está esperando tu ayuda Añade tu respuesta y gana puntos Nuevas preguntas de Matemáticas Mi yt es juancho1703river, si quiere suscríbase Uwu SUB X SUB 4 María José tenía 26 cerezas en un canasto, 27 en otro y 31 en otro, y las repartió entre 7 niños ¿Cuantas cerezas


How Do You Sketch The Region Enclosed By The Given Curves And Decide Whether To Integrate With Respect To X Or Y Then Find The Area Of The Region Of 2y 3x



Solve The Following Simultane See How To Solve It At Qanda
Proof f(x, y) = xy(x 2 − y 2) / (x 2 y 2) continuous everywhere Let f(x, y) = xy(x2 − y2) / (x2 y2) with f(0, 0) = 0 The question was asking to proof f(x, y) continuous everywhere One way to solve it was to just change x = rcos(θ), y = rsin(θ) and solved itSuppose the curves are x = y2 and x = 4 y2 and and you want to find points on the two curves with the same yvalue Then substitute y 2 from the first equation into the second to obtain x = 4 x So to achieve the same yvalue the xvalue on the second curve must be (minus) 4 times the xvalue on the first curve x = 4y2 and x = y2C) 2x y =d) 4x 5y 62=e) Xy x 2 =f) Xyz = Receba agora as respostas que você precisa!



If X 3 2x 2y 2 5x Y 5 0 And Y 1 1 Then A Y Prime 1 4



How Do You Find The Critical Points Of F X Y 10 X 2 2y 2 2y 4 2x Y 2 Socratic
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyQuestion Can you help me solve the equation (2x^2xyy^2=8)and(xy=4) I have to find the value of x and y I'm having trouble solving this particular problem I just know the answer has to have 4 solutions4) = 50 Example Find the maximum and minimum values of f(x;y;z) = x3y5zon the sphere x 2 y z = 1 Let g(x;y;z



Systems Engineering And Analysis Ppt Download
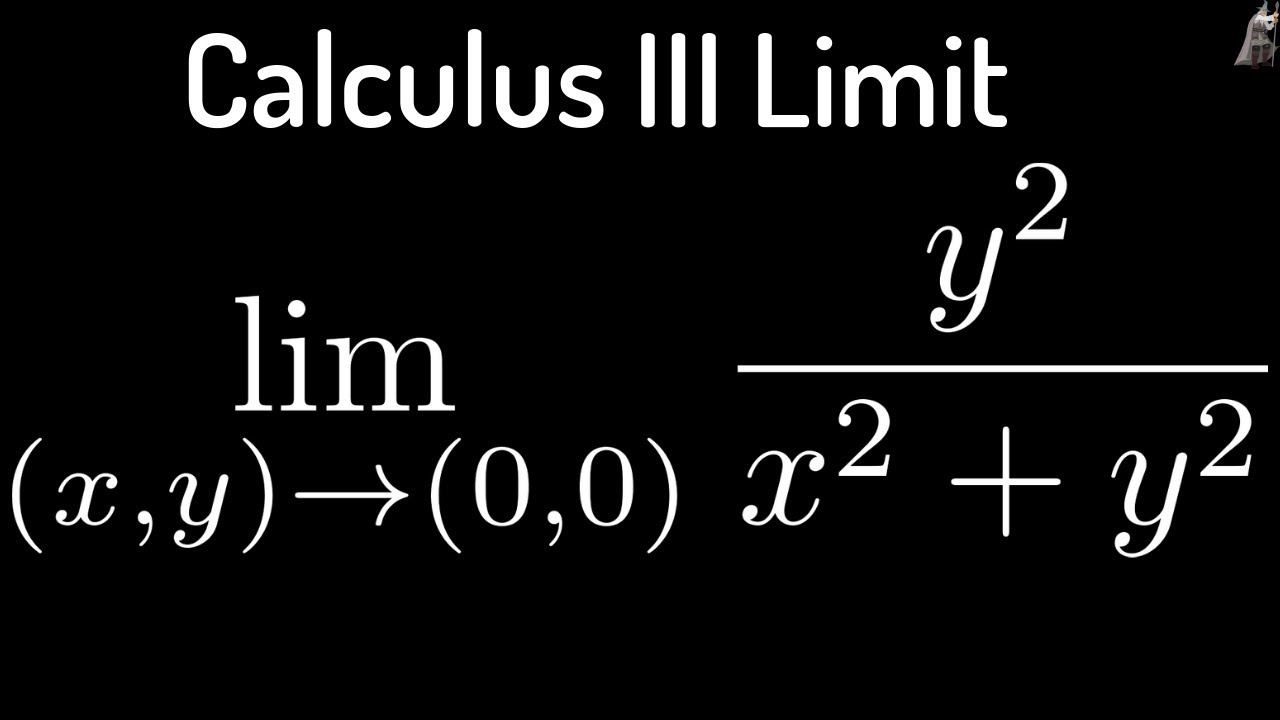


Multivariable Calculus Limit Of Y 2 X 2 Y 2 As X Y Approaches 0 0 Youtube
Search the world's information, including webpages, images, videos and more Google has many special features to help you find exactly what you're looking forNov , 11 · F(x,y) = 3xy x^2y xy^2 Maximum and minimum values and saddle points of the function So I understand that I have to find partial derivatives to respect to x and y to find the critical points ok, after I found the partial derivatives, I set them equal to 0 then I was stuck I don't know how to do substitution with the partial derivatives f_x(x,y) = 3y 2xy y^2 f_y(x,y) = 3x xMathf(x,y) = 2x^4 y^2 x^2 2y/math Our main task is to seek and solve the relative extrema if it exist We know that relative extrema occurs in conjunction with the following two condition, 1 math\triangledown f=0/math which implies t
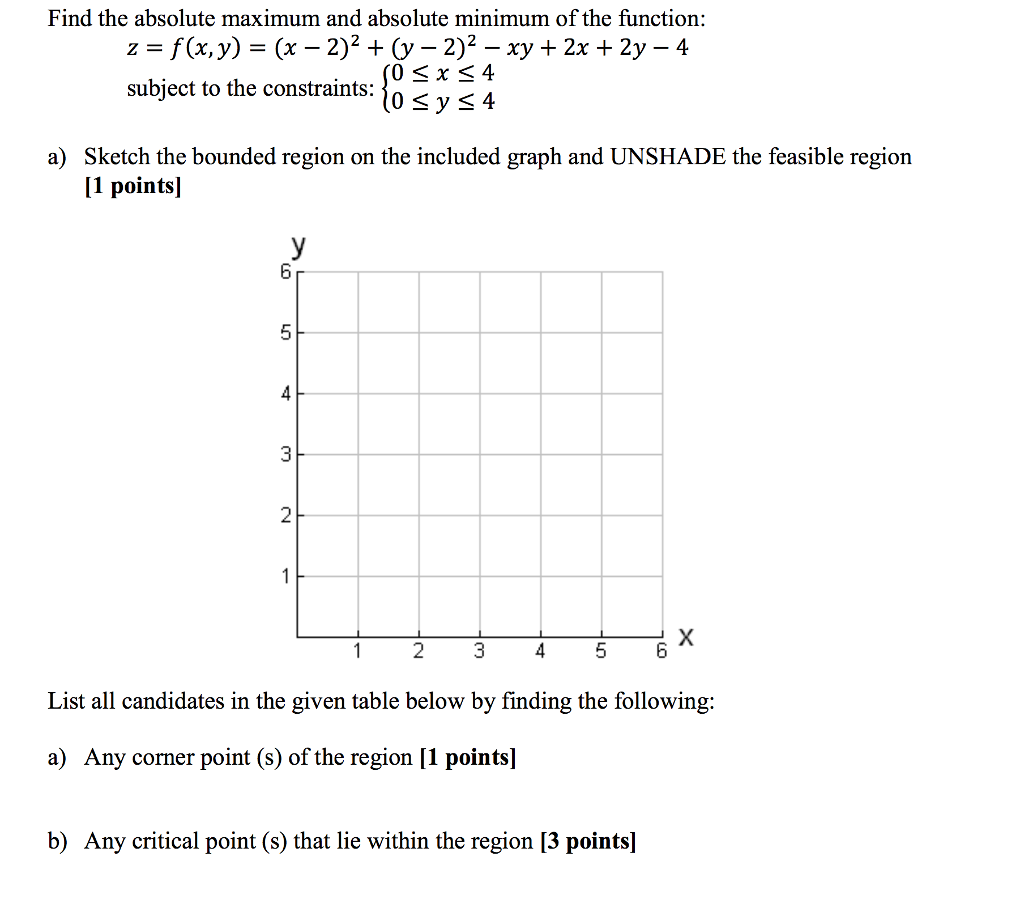


Solved Find The Absolute Maximum And Absolute Minimum Of Chegg Com



Systems Of Equations With Substitution 9x 3y 15 Y X 5 Video Khan Academy
43 x 2 2xy y 2 is a perfect square It factors into (xy)•(xy) which is another way of writing (xy) 2 How to recognize a perfect square trinomial • It has three terms • Two of its terms are perfect squares themselves • The remaining term is twice the product of the square roots of the other two terms Final result x • (2x yStep by Step Solution Step 1 Equation at the end of step 1 (((((x2)xy)4x)2y2)y)3 Step 2 Trying to factor by pulling out 21 Factoring x2xy4x2y2y3 Thoughtfully split the expression at hand into groups, each group having two terms Group 1 2y24xThe partial derivatives f x = 2x and f y = 2y 4 exist everywhere Therefore, local extreme values can occur only where f x = 2x = 0 and f y = 2y 4 = 0 The only possibility is the point (0;2), where the value of f is 5 Since f (x;y) = x2 (y 2)2 5 is never less than 5, we see that the critical point (0;2) gives a local minimum



If X 2y 8 And Xy 2 Then Find The Value Of X 2 4y 2 Brainly In



Solved 3 3 6 Marks 3 Attempt All Parts Step By Ste Chegg Com
All equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ± b 2 − 4 a c The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction y^ {2}xyx^ {2}=4 y 2 x y x 2 = 4 Subtract 4 from both sides of the equationPereiraellen4 está aguardando sua ajuda Inclua sua resposta e ganhe pontos(0 , 0) , (1 , 1) and (1 , 1) We now determine the second order partial derivatives f xx (x,y) = 4 f yy (x,y) = 12y 2 f xy (x,y) = 4 We now use a table to study the signs of D and f xx (a,b) and use the above theorem to decide on whether a given critical point is



Lagrange Multipliers Minimize F X Y X 2 Y 2 Subject To X 2y 5 0 Youtube



Solutions F X 6x 2 6xy 24x F Y 3x 2 6y To Find The Critical Points We Solve Pdf Free Download
Let f (x,y) = xy x^2 y^2 2x 2y 4 Find the gradient delta f (1,2) delta f (x,y) = (fx, fy) Fx = y 2x 2 Fy = x 2y 2 delta f (1,2) = ( y 2x 2, x 2y 2) delta f (1,2) = ( 2, 5) Find the directions of that Du f (1,2) = 0 u = (5,2) D = delta f (1,2) u
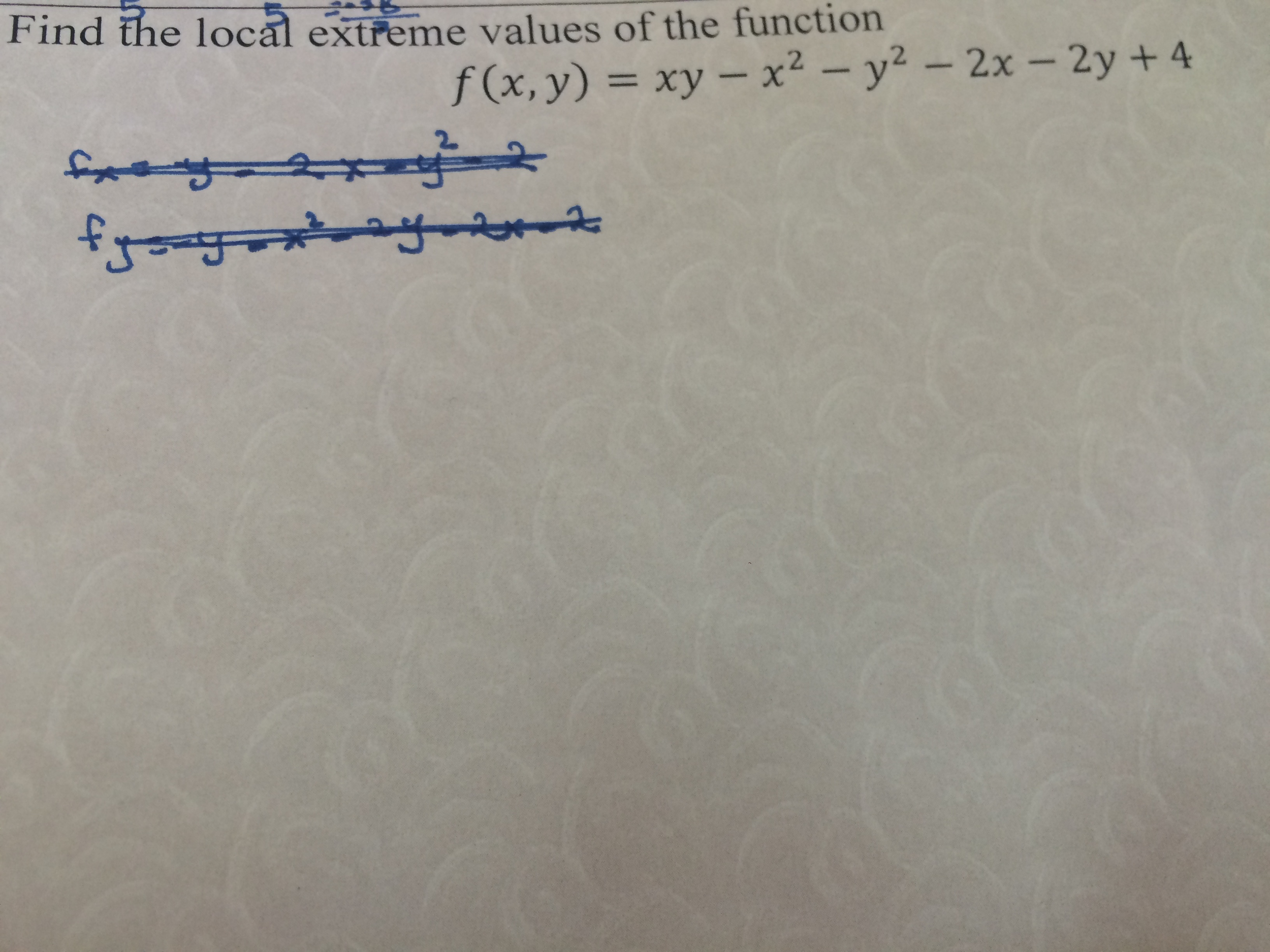


Solved Find The Local Extreme Value Of The Function F X Chegg Com



Engineering Mathematics Notes



Solved Find The Critical Points For The Function F X Y Chegg Com



Solved Y V1 X2 1 31 2 X Y 2 25 X Y 3 1 Chegg Com



Find The Asymptotes Of The Following Curves Y 3 X 2y 2x Y 2 2x



Example 15 Chapter 6 Solve X 2y 8 2x Y 8



Implicit Differentiation Advanced Example Video Khan Academy



Lagrange Multipliers Ppt Download


Can You Help Me How Do I Solve Y Y 2x 2 Dx 2 Y Dy 0 Quora



Consider The Function F X Y Ln X 2 Y 2 3 Compute The Partial Derivatives Of The First And Second Order Mathematics Stack Exchange



Engineering Mathematics Notes



Vector Analysis By Alimkanwalimtinaa Issuu



Ejercicios De Calculo Vectorial Pagina 2 Monografias Com



Math 432 Hw 2 4 Solutions



Find The Asymptotes Of The Following Curves Y 3 3x 2y X Y 2 3x 3 2y 2 2x Y 4x 5y 6 0 Youtube



Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange



Assignment 5 Man 001 Man 006 Studocu



Answered 3 7 Find The Second Partial Bartleby



14 2 Limits And Continuity
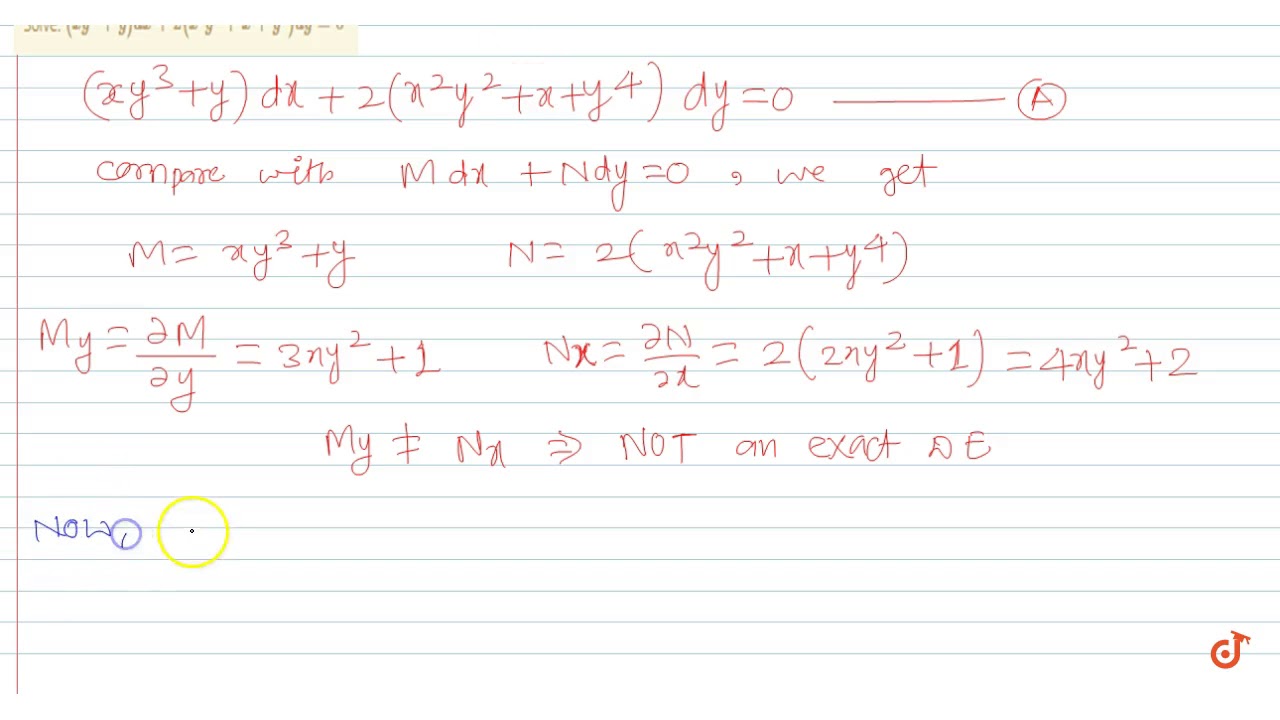


Solve Xy 3 Y Dx 2 X 2y 2 X Y 4 Dy 0 Youtube
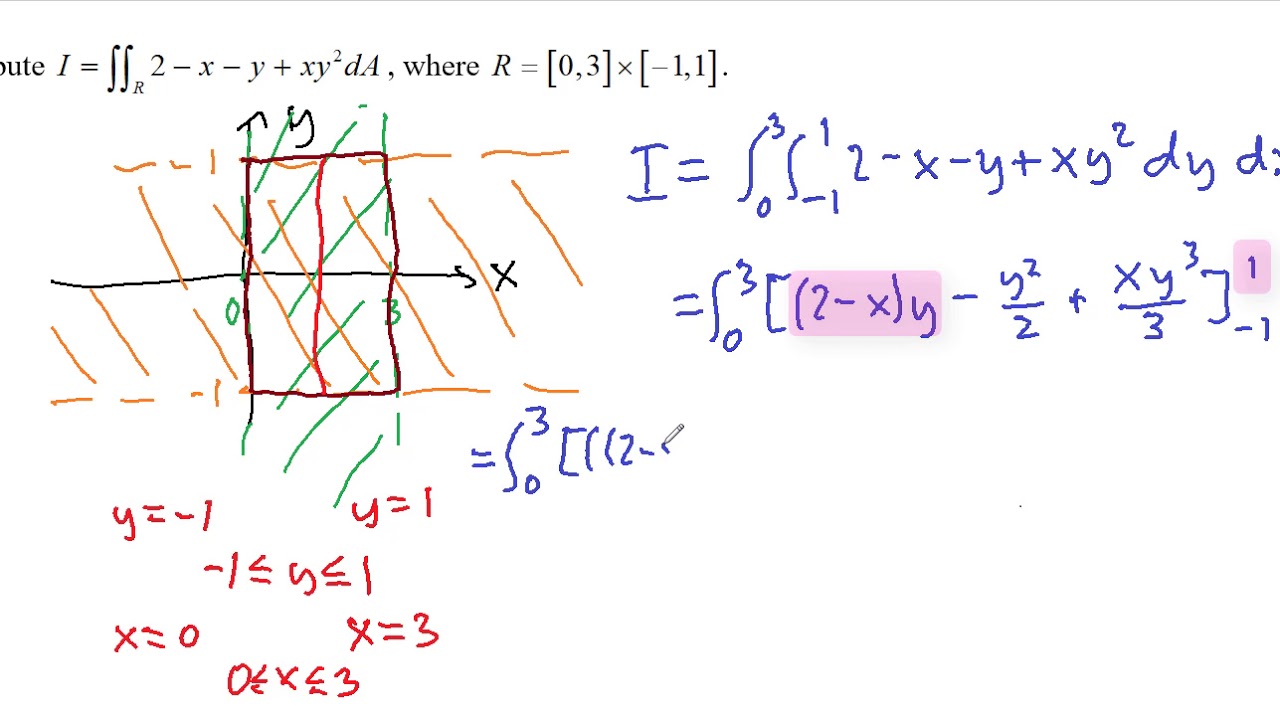


Double Integrals Volume And Average Value



Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange
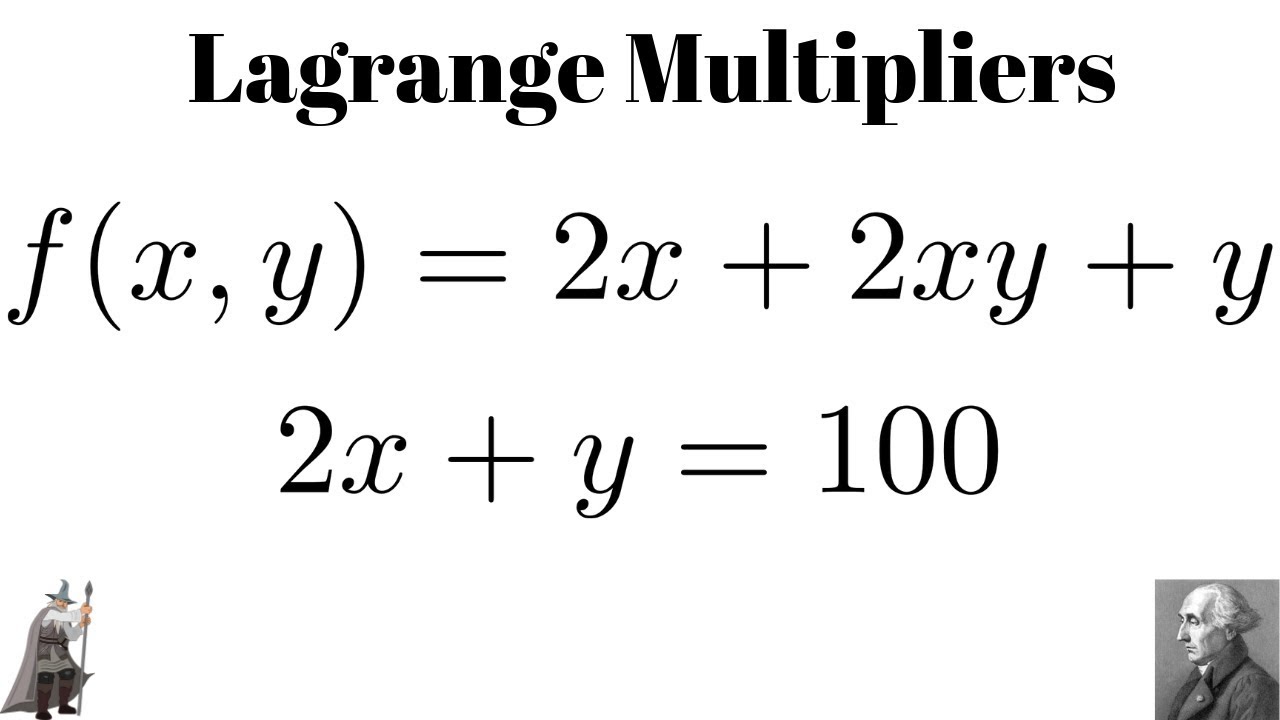


Lagrange Multipliers Maximize F X Y 2x 2xy Y Subject To 2x Y 100 Youtube



Maximum And Minimum Values Ppt Download



Solutions F X 6x 2 6xy 24x F Y 3x 2 6y To Find The Critical Points We Solve Pdf Free Download



Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange



How To Do Implicit Differentiation 7 Steps With Pictures



Local Maximum Minimum



0 件のコメント:
コメントを投稿